Introduction to LiDAR
LiDAR is a remote sensing technique that uses visible or near-infrared laser energy to measure the distance between a sensor and an object. LiDAR sensors are versatile and (often) mobile; they help autonomous cars avoid obstacles and make detailed topographic measurements from space. Before diving into LiDAR data processing, we will spend a bit of time reviewing some LiDAR fundamentals and discussing some terms of art.
Types of LiDAR
LiDAR systems, generally speaking, come in one of three types:
Pulse-based, or linear-mode, systems emit a pulse of laser energy and measure the time it takes for that energy to travel to a target, bounce off the target, and be returned to the sensor. These systems are called linear-mode because they (generally) only have a single aperture, and so can only measure distance along a single vector at any point in time. Pulse-based systems are very common, and are usually what you would think of when you think of LiDAR.
Phase-based LiDAR systems measure distance via interferometry, that is, by using the phase of a modulated laser beam to calculate a distance as a fraction of the modulated signal’s wavelength. Phase-based systems can be very precise, on the order of a few millimeters, but since they require comparatively more energy than the other two types they are usually used for short-range (e.g. indoor) scanning.
Geiger-mode, or photon-counting, systems use extremely sensitive detectors that can be triggered by a single photon. Since only a single photon is required to trigger a measurement, these systems can operate at much much higher altitudes than linear mode systems. However, Geiger-mode systems are relatively new and suffer from very high amounts of noise and other operational restrictions, making them significantly less common than linear-mode systems.
Note
Unless otherwise noted, if we talk about a LiDAR scanner in this program, we will be referring to a pulse-based (linear) system.
Modes of LiDAR Collection
LiDAR collects are generally categorized into four subjective types:
Terrestrial LiDAR Scanning (TLS): scanning with a stationary LiDAR sensor, usually mounted on a tripod.
Airborne LiDAR scanning (ALS): also called airborne laser swath mapping (ALSM), scanning with a LiDAR scanner mounted to a fixed-wing or rotor aircraft.
Mobile LiDAR scanning (MLS): scanning from a ground-based vehicle, such as a car.
Unmanned LiDAR scanning (ULS): scanning with drones or other unmanned vehicles.
With the exception of stationary TLS, LiDAR scanning generally requires the use of an integrated GNSS/IMU (Global Navigation Satellite System/Inertial Motion Unit), which provides information about the position, rotation, and motion of the scanning platform.
Note
As stated in the class description, we will focus on mobile and airborne laser scanning (MLS/ALS), though we will also use some TLS data.
Georeferencing
LiDAR scanners collect information in the Scanner’s Own Coordinate System (SOCS); this is a coordinate system centered at the scanner. The process of rotating, translating, and (possibly) transforming a point cloud into a real-world spatial reference system is known as georeferencing.
In the case of TLS, georeferencing is simply a matter of discovering the position and orientation of the static scanner. This is usually done with GNSS control points, which are used to solve for the scanner’s position via least-squares.
For mobile or airborne LiDAR scanning, it is necessary to merge the scanner’s points with the GNSS/IMU data. This can be done on-the-fly or as a part of a post-processing workflow. Since this is a common operation for mobile and airborne LiDAR collects, we will spend a moment discussing the methods and complications for georeferencing mobile LiDAR and GNSS/IMU data.
Integrating LiDAR and GNSS/IMU data
The LiDAR georeferencing equation is well-established; we present a version here from [Gle07]:
where:
\(\mathbf{p}^l_G\) are the coordinates of the target point in the global reference frame
\(\mathbf{p}^l_{GPS}\) are the coordinates of the GNSS sensor in the global reference frame
\(\mathbf{R}^l_b\) is the rotation matrix from the navigation frame to the global reference frame
\(\mathbf{R}^b_s\) is the rotation matrix from the scanner’s frame to the navigation frame (boresight matrix)
\(\mathbf{r}^s\) is the coordinates of the laser point in the scanner’s frame
\(\mathbf{l}^b\) is the lever-arm offset between the scanner’s original and the navigation’s origin
This equation contains fourteen unknowns, and in order to georeference a single LiDAR return we must determine all fourteen variables at the time of the pulse.
As a rule of thumb, the position, attitude, and motion of the scanning platform (aircraft, vehicle, etc) are sampled at a much lower rate than the pulse rate of the laser — rates of ~1Hz are common for GNSS/IMU sampling. In order to match the GNSS/IMU sampling rate with the sampling rate of the laser, GNSS/IMU measurements are interpolated to line up with the LiDAR measurements. Then, these positions and attitudes are combined via Equation (1) to create a final, georeferenced point cloud.
Note
While lever-arm offsets are usually taken from the schematic drawings of the LiDAR mounting system, the boresight matrix cannot be reliably determined from drawings alone. The boresight matrix must therefore be determined either via manual or automated boresight calibration using actual LiDAR data of planar surfaces, such as the roof and sides of buildings. The process for determining a boresight calibration from LiDAR data is beyond the scope of this class.
Discrete-Return vs. Full-Waveform
Pulse-based LiDAR systems use the round-trip travel time of a pulse of laser energy to measure distances. The outgoing pulse of a LiDAR system is roughly (but not exactly) a Gaussian:
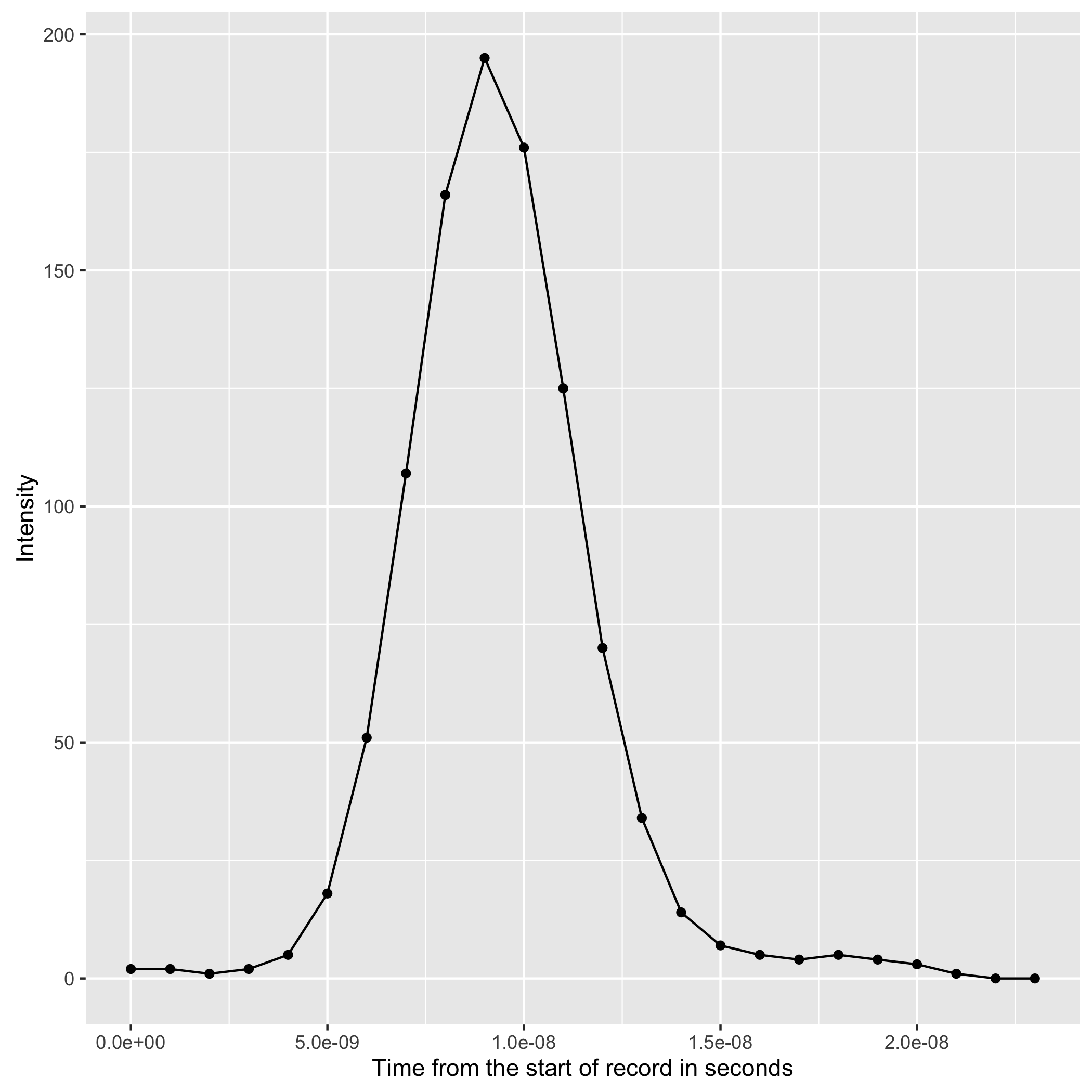
A real-world outgoing LiDAR pulse.
This pulse can interact with multiple objects in a scene before it is returned to the sensor. Here is an example of a LiDAR return:
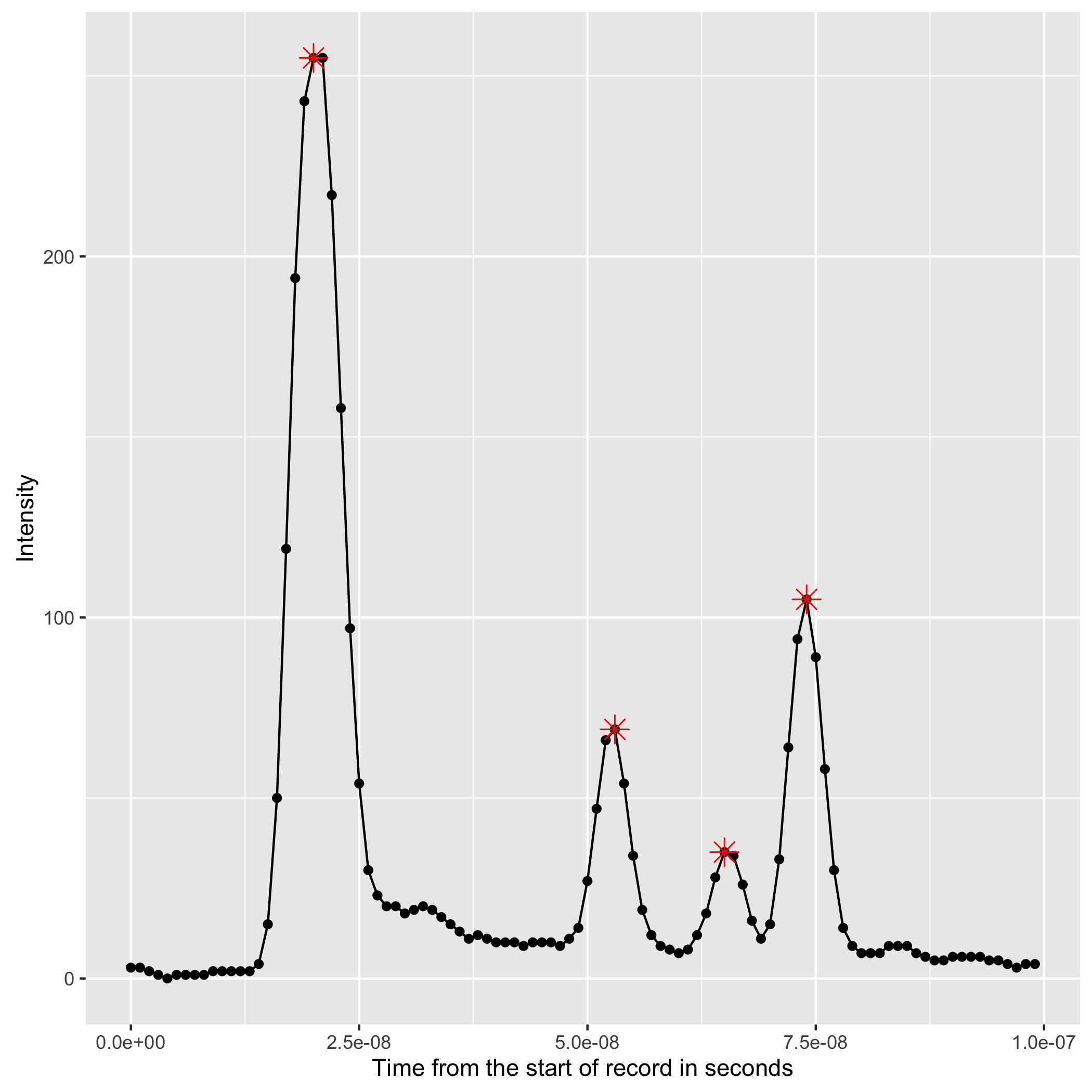
A real-world incoming LiDAR return. Potential discrete-return peaks are marked in red.
As you can see, this return pulse can be very complicated. While there is more information contained in the “full waveform” picture displayed above, many LiDAR consumers are only interested in detecting the presence or absence of an object — simplistically, the peaks in that waveform.
Full waveform data is used only in specialized circumstances. If you have or receive LiDAR data, it will usually be discrete return (point clouds). Processing full waveform data is beyond the scope of this class.
Note
PDAL is a discrete-return point cloud processing library. It does not have any functionality to analyze or process full waveform data.
Craig L. Glennie. Rigorous 3D error analysis of kinematic scanning LIDAR systems. Journal of Applied Geodesy, jan 2007.